Demystifying the Black Art of Software Estimation: What Is an "Estimate"?
- By Steve McConnell
- 2/22/2006
- Estimates, Targets, and Commitments
- Relationship Between Estimates and Plans
- Estimates as Probability Statements
- Estimation’s Real Purpose
Estimates as Probability Statements
If three-quarters of software projects overrun their estimates, the odds of any given software project completing on time and within budget are not 100%. Once we recognize that the odds of on-time completion are not 100%, an obvious question arises: “If the odds aren’t 100%, what are they?” This is one of the central questions of software estimation.
Software estimates are routinely presented as single-point numbers, such as “This project will take 14 weeks.” Such simplistic single-point estimates are meaningless because they don’t include any indication of the probability associated with the single point. They imply a probability as shown in Figure 1-1—the only possible outcome is the single point given.
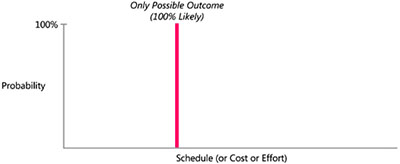
Figure 1-1 Single-point estimates assume 100% probability of the actual outcome equaling the planned outcome. This isn’t realistic.
A single-point estimate is usually a target masquerading as an estimate. Occasionally, it is the sign of a more sophisticated estimate that has been stripped of meaningful probability information somewhere along the way.
Accurate software estimates acknowledge that software projects are assailed by uncertainty from all quarters. Collectively, these various sources of uncertainty mean that project outcomes follow a probability distribution—some outcomes are more likely, some outcomes are less likely, and a cluster of outcomes in the middle of the distribution are most likely. You might expect that the distribution of project outcomes would look like a common bell curve, as shown in Figure 1-2.
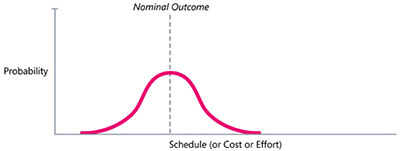
Figure 1-2 A common assumption is that software project outcomes follow a bell curve. This assumption is incorrect because there are limits to how efficiently a project team can complete any given amount of work.
Each point on the curve represents the chance of the project finishing exactly on that date (or costing exactly that much). The area under the curve adds up to 100%. This sort of probability distribution acknowledges the possibility of a broad range of outcomes. But the assumption that the outcomes are symmetrically distributed about the mean (average) is not valid. There is a limit to how well a project can be conducted, which means that the tail on the left side of the distribution is truncated rather than extending as far to the left as it does in the bell curve. And while there is a limit to how well a project can go, there is no limit to how poorly a project can go, and so the probability distribution does have a very long tail on the right.
Figure 1-3 provides an accurate representation of the probability distribution of a software project’s outcomes.
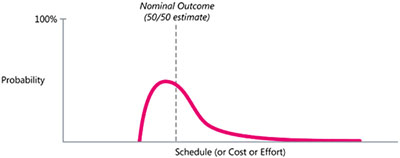
Figure 1-3 An accurate depiction of possible software project outcomes. There is a limit to how well a project can go but no limit to how many problems can occur.
The vertical dashed line shows the “nominal” outcome, which is also the “50/50” outcome—there’s a 50% chance that the project will finish better and a 50% chance that it will finish worse. Statistically, this is known as the “median” outcome.
Figure 1-4 shows another way of expressing this probability distribution. While Figure 1-3 showed the probabilities of delivering on specific dates, Figure 1-5 shows the probabilities of delivering on each specific date or earlier.
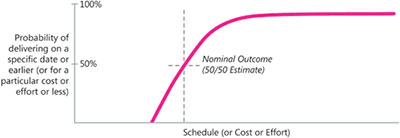
Figure 1-4 The probability of a software project delivering on or before a particular date (or less than or equal to a specific cost or level of effort).
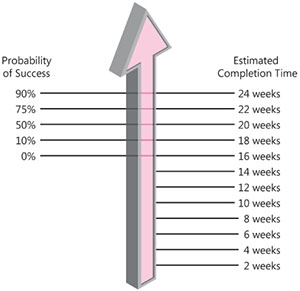
Figure 1-5 All single-point estimates are associated with a probability, explicitly or implicitly.
Figure 1-5 presents the idea of probabilistic project outcomes in another way. As you can see from the figure, a naked estimate like “18 weeks” leaves out the interesting information that 18 weeks is only 10% likely. An estimate like “18 to 24 weeks” is more informative and conveys useful information about the likely range of project outcomes.
You can express probabilities associated with estimates in numerous ways. You could use a “percent confident” attached to a single-point number: “We’re 90% confident in the 24-week schedule.” You could describe estimates as best case and worst case, which implies a probability: “We estimate a best case of 18 weeks and a worst case of 24 weeks.” Or you could simply state the estimated outcome as a range rather than a single-point number: “We’re estimating 18 to 24 weeks.” The key point is that all estimates include a probability, whether the probability is stated or implied. An explicitly stated probability is one sign of a good estimate.
You can make a commitment to the optimistic end or the pessimistic end of an estimation range—or anywhere in the middle. The important thing is for you to know where in the range your commitment falls so that you can plan accordingly.
Common Definitions of a “Good” Estimate
The answer to the question of what an “estimate” is still leaves us with the question of what a good estimate is. Estimation experts have proposed various definitions of a good estimate. Capers Jones has stated that accuracy with ±10% is possible, but only on well-controlled projects (Jones 1998). Chaotic projects have too much variability to achieve that level of accuracy.
In 1986, Professors S.D. Conte, H.E. Dunsmore, and V.Y. Shen proposed that a good estimation approach should provide estimates that are within 25% of the actual results 75% of the time (Conte, Dunsmore, and Shen 1986). This evaluation standard is the most common standard used to evaluate estimation accuracy (Stutzke 2005).
Numerous companies have reported estimation results that are close to the accuracy Conte, Dunsmore, and Shen and Jones have suggested. Figure 1-6 shows actual results compared to estimates from a set of U.S. Air Force projects.
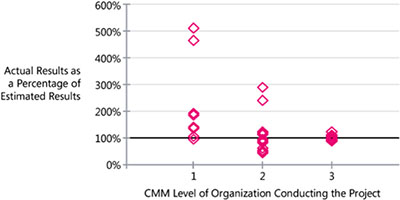
Source: “A Correlational Study of the CMM and Software Development Performance” (Lawlis, Flowe, and Thordahl 1995).
Figure 1-6 Improvement in estimation of a set of U.S. Air Force projects. The predictability of the projects improved dramatically as the organizations moved toward higher CMM levels.1
Figure 1-7 shows results of a similar improvement program at the Boeing Company.
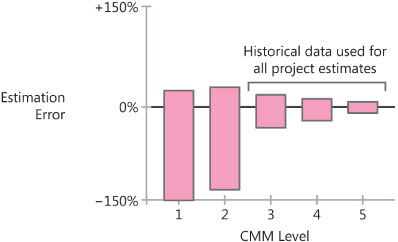
Figure 1-7 Improvement in estimation at the Boeing Company. As with the U.S. Air Force projects, the predictability of the projects improved dramatically at higher CMM levels.
A final, similar example, shown in Figure 1-8, comes from improved estimation results at Schlumberger.
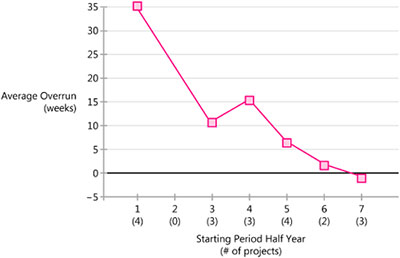
Figure 1-8 Schlumberger improved its estimation accuracy from an average overrun of 35 weeks to an average underrun of 1 week.
One of my client companies delivers 97% of its projects on time and within budget. Telcordia reported that it delivers 98% of its projects on time and within budget (Pitterman 2000). Numerous other companies have published similar results (Putnam and Myers 2003). Organizations are creating good estimates by both Jones’s definition and Conte, Dunsmore, and Shen’s definition. However, an important concept is missing from both of these definitions—namely, that accurate estimation results cannot be accomplished through estimation practices alone. They must also be supported by effective project control.
Estimates and Project Control
Sometimes when people discuss software estimation they treat estimation as a purely predictive activity. They act as though the estimate is made by an impartial estimator, sitting somewhere in outer space, disconnected from project planning and prioritization activities.
In reality, there is little that is pure about software estimation. If you ever wanted an example of Heisenberg’s Uncertainty Principle applied to software, estimation would be it. (Heisenberg’s Uncertainty Principle is the idea that the mere act of observing a thing changes it, so you can never be sure how that thing would behave if you weren’t observing it.) Once we make an estimate and, on the basis of that estimate, make a commitment to deliver functionality and quality by a particular date, then we control the project to meet the target. Typical project control activities include removing noncritical requirements, redefining requirements, replacing less-experienced staff with more-experienced staff, and so on. Figure 1-9 illustrates these dynamics.
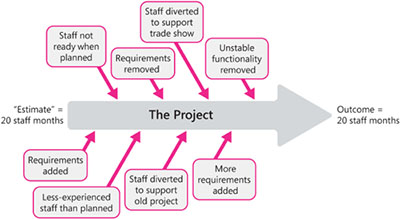
Figure 1-9 Projects change significantly from inception to delivery. Changes are usually significant enough that the project delivered is not the same as the project that was estimated. Nonetheless, if the outcome is similar to the estimate, we say the project met its estimate.
In addition to project control activities, projects are often affected by unforeseen external events. The project team might need to create an interim release to support a key customer. Staff might be diverted to support an old project, and so on.
Events that happen during the project nearly always invalidate the assumptions that were used to estimate the project in the first place. Functionality assumptions change, staffing assumptions change, and priorities change. It becomes impossible to make a clean analytical assessment of whether the project was estimated accurately—because the software project that was ultimately delivered is not the project that was originally estimated.
In practice, if we deliver a project with about the level of functionality intended, using about the level of resources planned, in about the time frame targeted, then we typically say that the project “met its estimates,” despite all the analytical impurities implicit in that statement.
Thus, the criteria for a “good” estimate cannot be based on its predictive capability, which is impossible to assess, but on the estimate’s ability to support project success, which brings us to the next topic: the Proper Role of Estimation.
