T-SQL Querying: TOP and OFFSET-FETCH

Median

Given a set of values, the median is the value below which 50 percent of the values fall. In other words, median is the 50th percentile. Median is such a classic calculation in the statistical analysis of data that many T-SQL solutions were created for it over time. I will focus on three solutions. The first uses the PERCENTILE_CONT window function. The second uses the ROW_NUMBER function. The third uses the OFFSET-FETCH filter and the APPLY operator.

Our calculation of median will be based on the continuous-distribution model. What this translates to is that when you have an odd number of elements involved, you should return the middle element. When you have an even number, you should return the average of the two middle elements. The alternative to the continuous model is the discrete model, which requires the returned value to be an existing value in the input set.

In my examples, I’ll use a table called T1 with groups represented by a column called grp and values represented by a column called val. You’re supposed to compute the median value for each group. The optimal index for median solutions is one defined on (grp, val) as the key elements. Use the following code to create the table and fill it with a small set of sample data to verify the validity of the solutions:

USE tempdb;
IF OBJECT_ID(N'dbo.T1', N'U') IS NOT NULL DROP TABLE dbo.T1;
GO

CREATE TABLE dbo.T1
(
  id  INT NOT NULL IDENTITY
    CONSTRAINT PK_T1 PRIMARY KEY,
  grp INT NOT NULL,
  val INT NOT NULL
);

CREATE INDEX idx_grp_val ON dbo.T1(grp, val);

INSERT INTO dbo.T1(grp, val)
  VALUES(1, 30),(1, 10),(1, 100),
        (2, 65),(2, 60),(2, 65),(2, 10);

Use the following code to populate the table with a large set of sample data (10 groups, with 1,000,000 rows each) to check the performance of the solutions:

DECLARE
  @numgroups AS INT = 10,
  @rowspergroup AS INT = 1000000;

TRUNCATE TABLE dbo.T1;

DROP INDEX idx_grp_val ON dbo.T1;

INSERT INTO dbo.T1 WITH(TABLOCK) (grp, val)
  SELECT G.n, ABS(CHECKSUM(NEWID())) % 10000000
  FROM TSQLV3.dbo.GetNums(1, @numgroups) AS G
    CROSS JOIN TSQLV3.dbo.GetNums(1, @rowspergroup) AS R;

CREATE INDEX idx_grp_val ON dbo.T1(grp, val);

Solution using PERCENTILE_CONT

Starting with SQL Server 2012, T-SQL supports window functions to compute percentiles. PERCENTILE_CONT implements the continuous model, and PERCENTILE_DISC implements the discrete model. The functions are not implemented as grouped, ordered set functions; rather, they are implemented as window functions. This means that instead of grouping the rows by the grp column, you will define the window partition based on grp. Consequently, the function will return the same result for all rows in the same partition instead of once per group. To get the result only once per group, you need to apply the DISTINCT option. Here’s the solution to compute median using the continuous model with PERCENTILE_CONT:

SELECT
  DISTINCT grp, PERCENTILE_CONT(0.5) WITHIN GROUP(ORDER BY val) OVER(PARTITION BY grp) AS median
FROM dbo.T1;

After you overcome the awkwardness in using a window function instead of a grouped one, you might find the solution agreeable because of its simplicity and brevity. That’s until you actually run it and look at its execution plan (which is not for the faint of heart). The plan for the solution is very long and inefficient. It does two rounds of spooling the data in work tables, reading each spool twice—once to get the detail and once to compute aggregates. It took the solution 79 seconds to complete in my system against the big set of sample data. If good performance is important to you, you should consider other solutions.

Solution using ROW_NUMBER

The second solution defines two CTEs. One called Counts is based on a grouped query that computes the count (column cnt) of rows per group. Another is called RowNums, and it computes row numbers (column n) for the detail rows. The outer query joins Counts with RowNums, and it filters only the relevant values for the median calculation. (Keep in mind that that the relevant values are those where n is (cnt+1)/2 or (cnt+2)/2, using integer division.) Finally, the outer query groups the remaining rows by the grp column and computes the average of the val column as the median. Here’s the complete solution:

WITH Counts AS
(
  SELECT grp, COUNT(*) AS cnt
  FROM dbo.T1
  GROUP BY grp
),
RowNums AS
(
  SELECT grp, val,
    ROW_NUMBER() OVER(PARTITION BY grp ORDER BY val) AS n
  FROM dbo.T1
)
SELECT C.grp, AVG(1. * R.val) AS median
FROM Counts AS C
  INNER MERGE JOIN RowNums AS R
    on C.grp = R.grp
WHERE R.n IN ( ( C.cnt + 1 ) / 2, ( C.cnt + 2 ) / 2 )
GROUP BY C.grp;

The plan for this solution is shown in Figure 5-12.

FIGURE 5-12 Plan for a solution using ROW_NUMBER.

SQL Server chose a serial plan that performs two scans of the index, a couple of order-based aggregates, a computation of row numbers, and a merge join. Compared to the previous solution with the PERCENTILE_CONT function, the new solution is quite efficient. It took only 8 seconds to complete in my system. Still, perhaps there’s room for further improvements. For example, you could try to come up with a solution that uses a parallel plan, you could try to reduce the number of pages that need to be scanned, and you could try to eliminate the fairly expensive merge join.

Solution using OFFSET-FETCH and APPLY

The third solution I’ll present uses the APPLY operator and the OFFSET-FETCH filter. The solution defines a CTE called C, which is based on a grouped query that computes for each group parameters for the OFFSET and FETCH clauses based on the group count. The offset value (call it ov) is computed as (count – 1) / 2, and the fetch value (call it fv) is computed as 2 – count % 2. For example, if you have a group with 11 rows, ov is 5 and fv is 1. For a group with 12 rows, ov is 5 and fv is 2. The outer query applies to each group in C an OFFSET-FETCH query that retrieves the relevant values. Finally, the outer query groups the remaining rows and computes the average of the values as the median.

WITH C AS
(
  SELECT grp,
    COUNT(*) AS cnt,
    (COUNT(*) - 1) / 2 AS ov,
    2 - COUNT(*) % 2 AS fv
  FROM dbo.T1
  GROUP BY grp
)
SELECT grp, AVG(1. * val) AS median
FROM C
  CROSS APPLY ( SELECT O.val
                FROM dbo.T1 AS O
                where O.grp = C.grp
                order by O.val
                OFFSET C.ov ROWS FETCH NEXT C.fv ROWS ONLY ) AS A
GROUP BY grp;

The plan for this solution is shown in Figure 5-13.

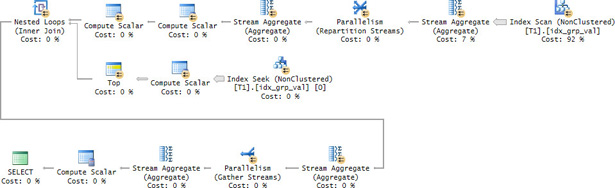
FIGURE 5-13 Plan for a solution using OFFSET-FETCH and APPLY.

The plan for the third solution has three advantages over the plan for the second. One is that it uses parallelism efficiently. The second is that the index is scanned in total one and a half times rather than two. The cost of the seeks is negligible here because the data has dense groups. The third advantage is that there’s no merge join in the plan. It took only 1 second for this solution to complete on my system. That’s quite impressive for 10,000,000 rows.